APMC2025 | 4D-STEM workshop

Georgios Varnavides

Workshop

Contents

In Multislice Algorithm we introduced a very powerful and flexible algorithm for performing electron scattering simulations. Multislice STEM simulations, however, can be very computationally expensive since the converged electron probe needs to be transmitted/propagated at each scan position. In this section, we introduce an alternative formalism called planewave reciprocal-space interpolated scattering matrix (PRISM), which can achieve a significant speedup at a minor cost to accuracy Ophus, 2017.

Planewave Wavefunction Expansion¶

We start our PRISM algorithm exploration by noting that any electron wavefunction $\psi(\bm{r})$ can be written as a linear combination of planewaves:

\psi(\bm{r}) = \sum_{n,m} C_{n,m} S_{n,m}(\bm{r}),

(6.1)

where

S_{n,m}(\bm{r}) = \mathrm{exp} \left[-2\pi\,\mathrm{i}\, \bm{q}_{n,m} \cdot \bm{r} \right]

(6.2)

is a planewave with wavevector $\bm{q}_{n,m} = \left(n \Delta k_x, m \Delta k_y\right)$ for integer $(n,m)$ combinations and $\Delta k_x, \Delta k_y$ defined according to Sampling Considerations. The complex-valued coefficients $C_{n,m}$ are given by:

\begin{align} C_{n,m}(\bm{r}) & = A(\bm{q}_{n,m}) \mathrm{exp}\left[-\mathrm{i}\,\chi(\bm{q}_{n,m}) \right] \\ & \quad \times \mathrm{exp} \left[ -2\pi\, \mathrm{i} \, \bm{q_{n,m}} \cdot \left\{x - h\, \mathrm{tan}(\lambda(U_0)\, q_x), y - h\, \mathrm{tan}(\lambda(U_0)\,q_y) \right\} \right], \end{align}

(6.3)

where $h$ is the cell thickness, and $A(\bm{q})$ and $\chi(\bm{q})$ are the probe aperture and aberration functions defined in Electron Wavefunctions. The first line in (6.3) limits the maximum transferred spatial frequency and imparts any aberrations to the probe, while the second line applies a phase ramp to center the probe on the appropriate scan position.

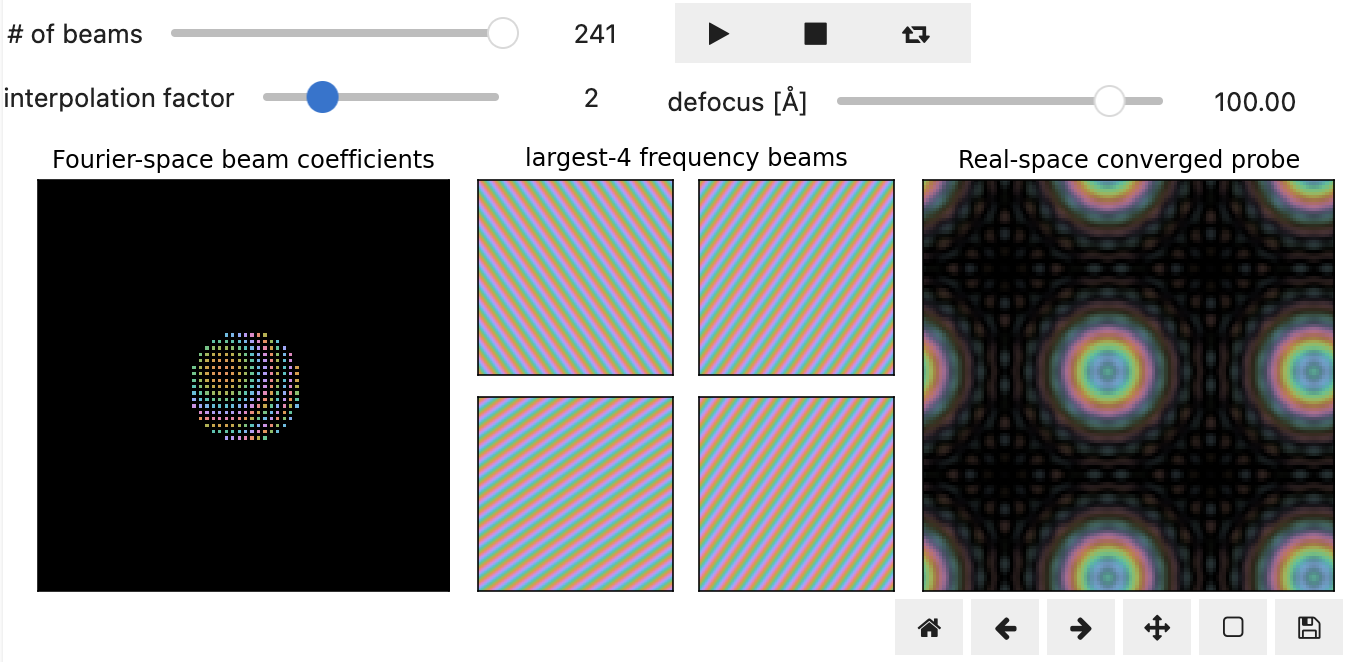
Figure 6.1 illustrates the above equations interactively. Try increasing the number of planewave beams to understand how increasingly higher-frequency planewaves are accumulated to construct the converged electron probe.

Multislice Operator Linearity¶

Substituting (6.1) into (5.11) we obtain:

\begin{align} \psi_{N}(\bm{r}) & = \mathcal{M}_{N-1} \mathcal{M}_{N-2} \dots \mathcal{M}_0 \sum_{n,m} C_{n,m} S_{n,m}(\bm{r}) \\ & = \sum_{n,m} C_{n,m} \mathcal{M}_{N-1} \mathcal{M}_{N-2} \dots \mathcal{M}_0 S_{n,m}(\bm{r}). \end{align}

(6.4)

The last line follows from the linearity of the multislice operator (being composed of linear convolutions), and highlights the numerical scheme for the PRISM algorithm:

The scattering matrix is pre-computed by applying the multislice operator to a set of planewaves.
The scattering matrix is reduced to specific probe positions and aberrations by taking the inner product with complex coefficients.

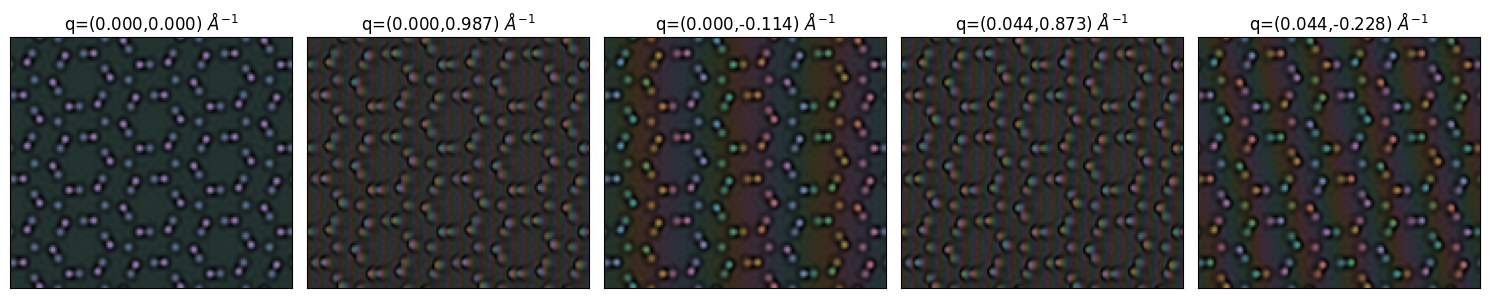
Figure 6.2 highlights the multislice operaration on 5 planewaves using different wavevectors, as they traverse the Si₃N₄ potential we have explored before. Notice that in-addition to the potential imprints, each planewave has a different phase-ramp.

Scattering Matrix Interpolation¶

Performing the multislice operation on a subset of planewaves, as-opposed to each scan probe position, can already result in speedups for simulations with many probe positions, at no accuracy cost. You might have however noticed an interpolation factor slider in Figure 6.1, which demonstrates the power of the PRISM algorithm.

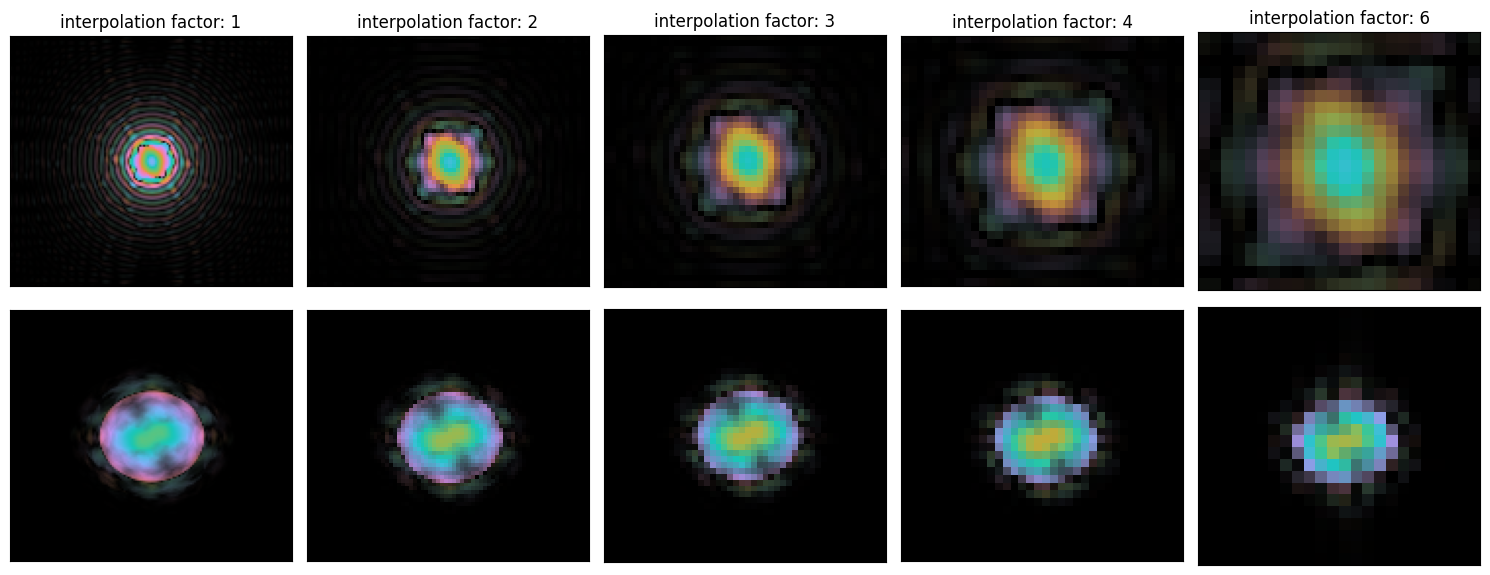
Instead of using every planewave inside the probe aperture, we can instead perform the expansion with every n $^{\mathrm{th}}$ probe. This is mathematically equivalent to Fourier downsampling of our wavefunction. While this can lead to significant speedups, it comes at a cost to accuracy.
Figure 6.3 demonstrates the effect of the interpolation factor on the reduction step of the PRISM algorithm.

References¶

Ophus, C. (2017). A fast image simulation algorithm for scanning transmission electron microscopy. Advanced Structural and Chemical Imaging, 3(1). 10.1186/s40679-017-0046-1

Electron Scattering Algorithms

Multislice Algorithm

Electron Scattering Algorithms

Bloch Wave Algorithm

[cite-Ophus_2017] Ophus, C. (2017). A fast image simulation algorithm for scanning transmission electron microscopy. Advanced Structural and Chemical Imaging, 3(1). 10.1186/s40679-017-0046-1

PRISM Algorithm

Planewave Wavefunction Expansion¶

Multislice Operator Linearity¶

Scattering Matrix Interpolation¶