Curvenote
Workshop

APMC2025 | 4D-STEM workshop

Contents

Direct Ptychography Tutorial 03

Open In Colab

This is the third and last tutorial notebook in the direct ptychography series.
In this tutorial notebook we will cover:

  • Optimum bright-field STEM reconstructions
  • Wigner distribution deconvolution reconstructions
  • Segmented-detector reconstructions

Downloads

This tutorial uses the following datasets:

Last updated: 2024 Feb 01

Introduction

So far, we have only used the (phase-compensated) single-side band (SSB) method. There are two closely-related techniques which have been proposed to perform better for low-dose datasets. Those are:

%pip install py4DSTEM > /dev/null 2>&1
import numpy as np
import py4DSTEM
import matplotlib.pyplot as plt

print(py4DSTEM.__version__)
%matplotlib inline
cupyx.jit.rawkernel is experimental. The interface can change in the future.

0.14.18

We’ll use the same, in-focus, dataset as the one we used in direct_ptychography_01.ipynb.

# Get the 4DSTEM data
py4DSTEM.io.gdrive_download(
    id_ = 'https://drive.google.com/uc?id=1Ml1Ga4-U0ZcTJxq0LVyTJDIVfnBuyd81',
    destination = '/content/',
    filename = 'dpc_STO_simulation.h5',
    overwrite=True
)
Downloading...
From: https://drive.google.com/uc?id=1Ml1Ga4-U0ZcTJxq0LVyTJDIVfnBuyd81
To: /content/dpc_STO_simulation.h5
100%|██████████| 75.5M/75.5M [00:00<00:00, 139MB/s]

file_path = '/content/'
file_data = file_path + 'dpc_STO_simulation.h5'

dataset = py4DSTEM.read(file_data)
dataset.crop_Q((24,-24,24,-24))
DataCube( A 4-dimensional array of shape (32, 32, 48, 48) called 'datacube', with dimensions: Rx = [0.0,0.12328531250000001,0.24657062500000002,...] A Ry = [0.0,0.12328531250000001,0.24657062500000002,...] A Qx = [0.0,1.0595062826244177,2.1190125652488354,...] mrad Qy = [0.0,1.0595062826244177,2.1190125652488354,...] mrad )

SSB Algorithm Variants

First, let’s reproduce the phase-compensated SSB reconstruction from direct_ptychography_01.ipynb:

energy = 200e3
semiangle_cutoff = 20

ssb = py4DSTEM.process.phase.SSB(
    energy=energy,
    datacube=dataset,
    semiangle_cutoff=semiangle_cutoff,
    verbose=True,
).preprocess(
    plot_center_of_mass=False,
    plot_rotation=False,
    plot_overlap_trotters=False,
    force_com_rotation=-15,
    crop_around_bf_disk=False,
).reconstruct(
).visualize(
)
Calculating center of mass: 100%|██████████| 1024/1024 [00:00<00:00, 8019.79probe position/s]
Best fit rotation forced to -15 degrees.
Normalizing amplitudes: 100%|██████████| 1024/1024 [00:01<00:00, 617.03probe position/s]
100%|██████████| 1024/1024 [00:02<00:00, 342.46it/s]
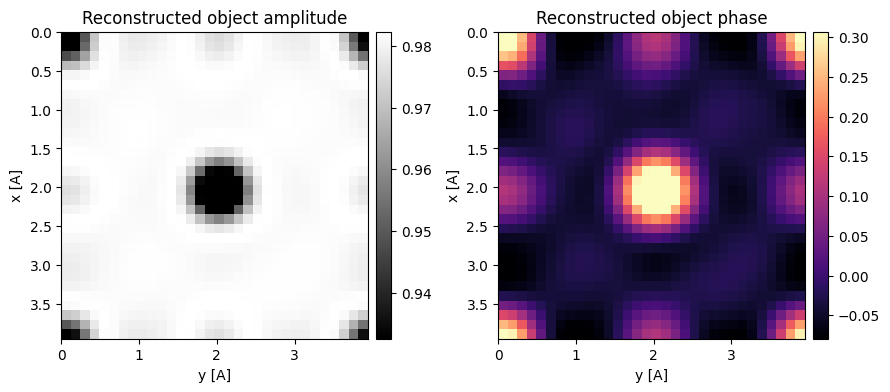
<Figure size 900x400 with 4 Axes>

Optimum bright-field (OBF) STEM also compensates for the phase in the double minus triple overlap trotters, albeit using a different normalization.
In py4DSTEM, this can be invoked using the OBF class.

obf = py4DSTEM.process.phase.OBF(
    energy=energy,
    datacube=dataset,
    semiangle_cutoff=semiangle_cutoff,
    verbose=True,
).preprocess(
    plot_center_of_mass=False,
    plot_rotation=False,
    plot_overlap_trotters=False,
    force_com_rotation=-15,
    crop_around_bf_disk=False,
).reconstruct(
).visualize(
)
Calculating center of mass: 100%|██████████| 1024/1024 [00:00<00:00, 43286.88probe position/s]
Best fit rotation forced to -15 degrees.
Normalizing amplitudes: 100%|██████████| 1024/1024 [00:00<00:00, 2736.99probe position/s]
100%|██████████| 1024/1024 [00:01<00:00, 922.49it/s]
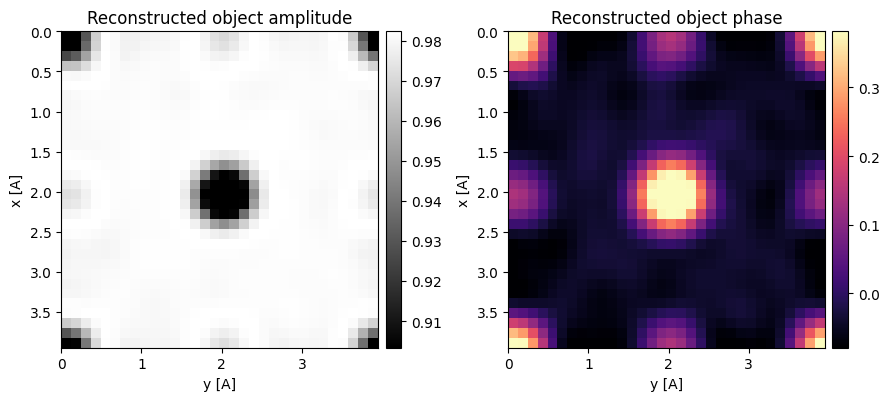
<Figure size 900x400 with 4 Axes>

Wigner distribution deconvolution (WDD) is a more involved technique which attempts to fully deconvolve the effects of the probe from the object.
The method uses a Wiener-filter to avoid dividing by zero and boosting noise.

It can be invoked in py4DSTEM using the WDD class and requires the user specify the (relative) Wiener filtering parameter (with reasonable values between 0.01 - 0.1).

wdd = py4DSTEM.process.phase.WDD(
    energy=energy,
    datacube=dataset,
    semiangle_cutoff=semiangle_cutoff,
    verbose=True,
).preprocess(
    plot_center_of_mass=False,
    plot_rotation=False,
    plot_overlap_trotters=False,
    force_com_rotation=-15,
    crop_around_bf_disk=False,
).reconstruct(
    relative_wiener_epsilon=0.01,
).visualize(
)
Calculating center of mass: 100%|██████████| 1024/1024 [00:00<00:00, 45614.47probe position/s]
Best fit rotation forced to -15 degrees.
Normalizing amplitudes: 100%|██████████| 1024/1024 [00:00<00:00, 2819.14probe position/s]
100%|██████████| 1024/1024 [00:01<00:00, 1171.38it/s]
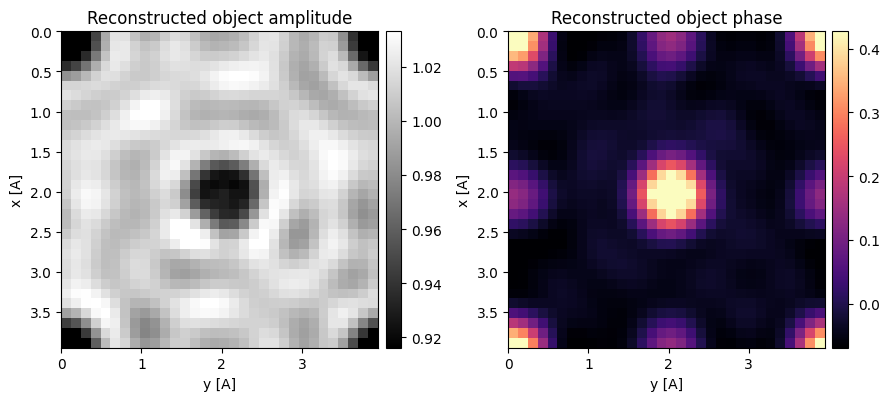
<Figure size 900x400 with 4 Axes>

The reconstructions all look quite similar, with OBF and WDD showing (slightly) higher information limits

fig, axs = plt.subplots(2,3,figsize=(12,8))

for ax, arr, title in zip(
    axs[0],
    (np.angle(ssb.object),np.angle(obf.object),np.angle(wdd.object)),
    ('reconstructed phase (SSB)','reconstructed phase (OBF)','reconstructed phase (WDD)')
):
    py4DSTEM.show(
        np.tile(arr,(2,2)),
        figax=(fig,ax),
        cmap='turbo',
        ticks=False,
        title=title,
    )

for ax, arr in zip(
    axs[1],
    (np.angle(ssb.object),np.angle(obf.object),np.angle(wdd.object))
):
    py4DSTEM.show(
        np.tile(arr,(2,2)),
        figax=(fig,ax),
        cmap='turbo',
        show_fft=True,
        apply_hanning_window=False,
        ticks=False,
    )

fig.tight_layout()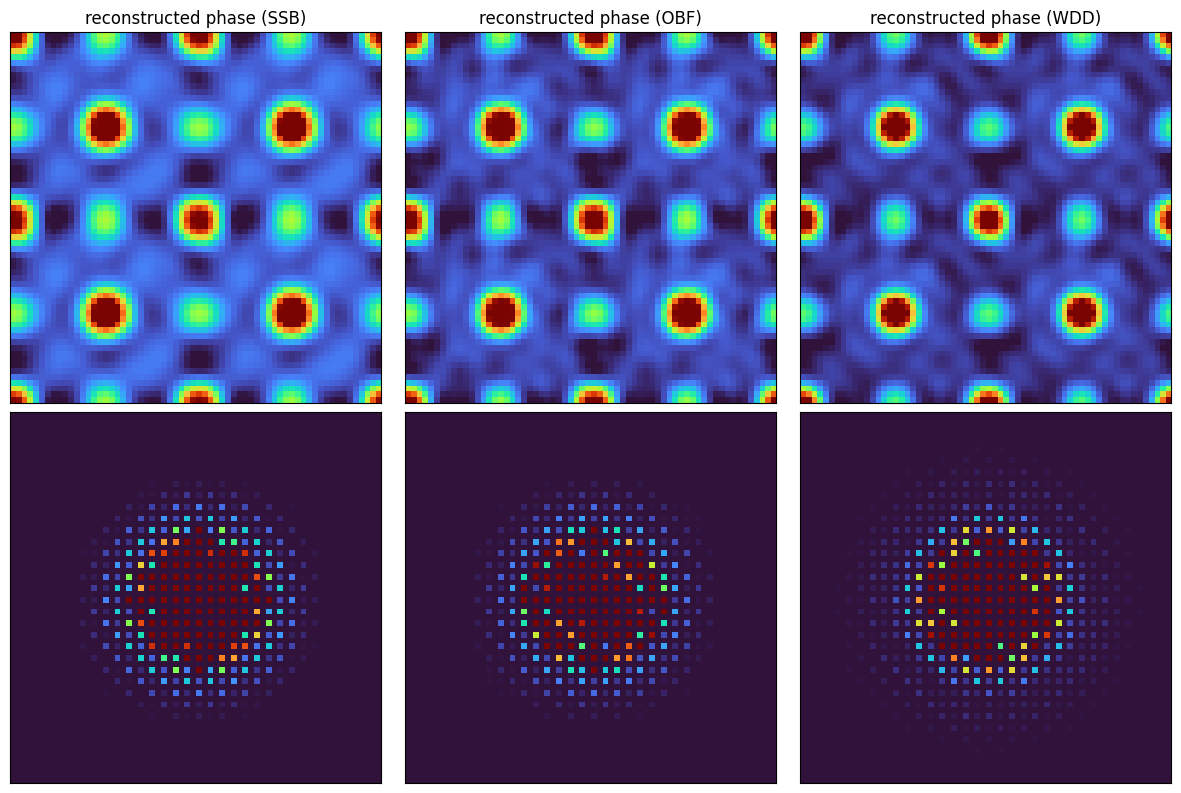
<Figure size 1200x800 with 6 Axes>

Segmented Detector Datasets

SSB and OBF are additionally very useful in post-processing segmented-detector datasets.
To see this, we’ll post-process our 4D-data using an annular detector with 6 segments.

def annular_segmented_detectors(
    energy,
    gpts,
    sampling,
    n_angular_bins,
    rotation_offset = 0,
    inner_radius = 0,
    outer_radius = np.inf,
):
    """ """
    nx,ny = gpts
    sx,sy = sampling
    wavelength = py4DSTEM.process.utils.electron_wavelength_angstrom(energy)

    alpha_x = np.fft.fftfreq(nx,sx)*wavelength
    alpha_y = np.fft.fftfreq(ny,sy)*wavelength

    alpha = np.sqrt(alpha_x[:,None]**2 + alpha_y[None,:]**2)
    radial_mask = ((inner_radius*1e-3 <= alpha) & (alpha < outer_radius*1e-3))

    theta = (np.arctan2(alpha_y[None,:], alpha_x[:,None]) + rotation_offset) % (2 * np.pi)
    angular_bins = np.floor(n_angular_bins * (theta / (2 * np.pi))) + 1
    angular_bins *= radial_mask.astype("int")

    angular_bins = [np.fft.fftshift((angular_bins == i).astype("int")) for i in range(1,n_angular_bins+1)]
    return angular_bins

def create_segmented_4d_dataset_using_virtual_detectors(dc,masks):
    """ """

    masks_np = np.array(masks).astype(np.bool_)

    preprocessed_data = np.zeros(dc.shape,dtype=np.float32)
    for mask in masks_np:
        val = np.sum(dc.data*mask,axis=(-1,-2)) / np.sum(mask)
        preprocessed_data[...,mask] = val[:,:,None]

    preprocessed_dataset = py4DSTEM.DataCube(preprocessed_data,calibration=dc.calibration.copy())
    return preprocessed_dataset

segmented_detector_masks = annular_segmented_detectors(
    energy=energy,
    gpts=dataset.Qshape,
    sampling=ssb.sampling,
    n_angular_bins = 4,
    inner_radius = semiangle_cutoff/2,
    outer_radius=semiangle_cutoff,
)

segmented_dataset = create_segmented_4d_dataset_using_virtual_detectors(dataset,segmented_detector_masks)

We plot the mean diffraction pattern alongside the segmented detector masks to emphasize the vast reduction in information encoded in this dataset:

fig, axs = plt.subplots(1,3,figsize=(12,4))

py4DSTEM.show(
    dataset.data.mean((0,1)),
    ticks=False,
    figax=(fig,axs[0]),
    title="mean diffraction pattern",
)

py4DSTEM.show(
    segmented_detector_masks,
    combine_images=True,
    ticks=False,
    figax=(fig,axs[1]),
    title="segmented detector masks",
)

py4DSTEM.show(
    segmented_dataset.data.mean((0,1)),
    combine_images=True,
    ticks=False,
    figax=(fig,axs[2]),
    title="mean segmented pattern",
    vmin=0,vmax=1,
)

fig.tight_layout()
<Figure size 1200x400 with 3 Axes>

We can then use this pre-processed DataCube in the SSB and OBF classes, by passing a virtual_detector_masks argument in reconstruct.
Note this accepts “corner-centered” masks.

corner_centered_segmented_detector_masks = [np.fft.fftshift(mask.astype(np.bool_)) for mask in segmented_detector_masks]

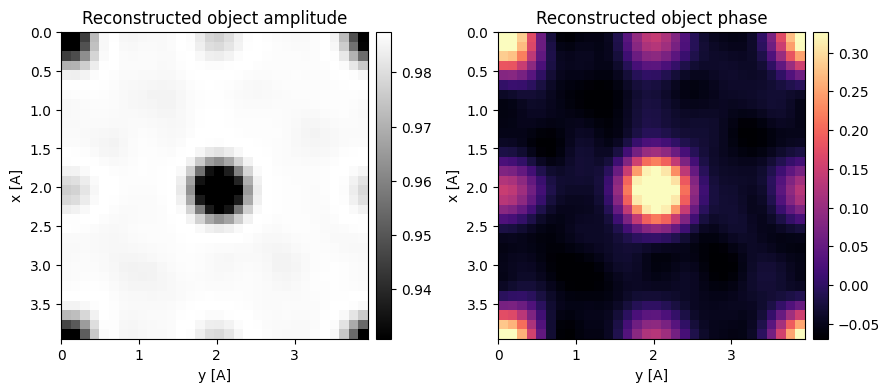
segmented_ssb = py4DSTEM.process.phase.SSB(
    energy=energy,
    datacube=segmented_dataset,
    semiangle_cutoff=semiangle_cutoff,
    verbose=True,
).preprocess(
    plot_center_of_mass=False,
    plot_rotation=False,
    plot_overlap_trotters=False,
    force_com_rotation=-15,
    crop_around_bf_disk=False,
).reconstruct(
    virtual_detector_masks=corner_centered_segmented_detector_masks,
).visualize(
)
Calculating center of mass: 100%|██████████| 1024/1024 [00:00<00:00, 46086.31probe position/s]
Best fit rotation forced to -15 degrees.
Normalizing amplitudes: 100%|██████████| 1024/1024 [00:00<00:00, 2797.24probe position/s]
100%|██████████| 1024/1024 [00:01<00:00, 775.09it/s]
<Figure size 900x400 with 4 Axes>
segmented_obf = py4DSTEM.process.phase.OBF(
    energy=energy,
    datacube=segmented_dataset,
    semiangle_cutoff=semiangle_cutoff,
    verbose=True,
).preprocess(
    plot_center_of_mass=False,
    plot_rotation=False,
    plot_overlap_trotters=False,
    force_com_rotation=-15,
    crop_around_bf_disk=False,
).reconstruct(
    virtual_detector_masks=corner_centered_segmented_detector_masks,
).visualize(
)
Calculating center of mass: 100%|██████████| 1024/1024 [00:00<00:00, 20018.12probe position/s]
Best fit rotation forced to -15 degrees.
Normalizing amplitudes: 100%|██████████| 1024/1024 [00:00<00:00, 1758.27probe position/s]
100%|██████████| 1024/1024 [00:02<00:00, 440.38it/s]
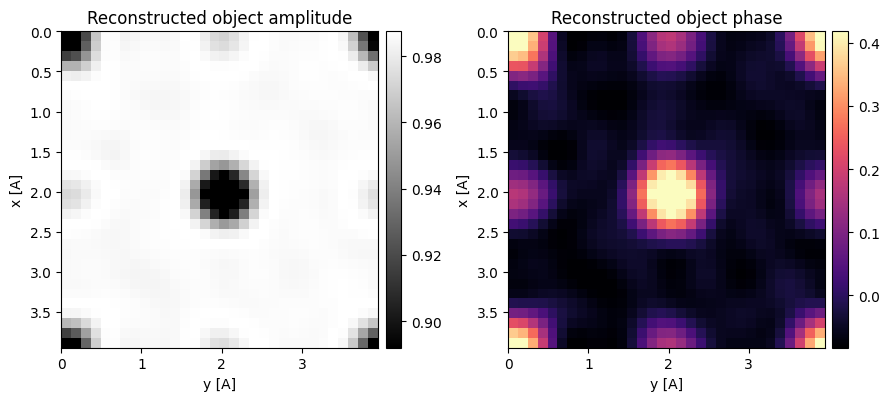
<Figure size 900x400 with 4 Axes>

Indeed, the methods still work remarkably well!

fig, axs = plt.subplots(2,2,figsize=(8,8))

for ax, arr, title in zip(
    axs[0],
    (np.angle(segmented_ssb.object),np.angle(segmented_obf.object)),
    ('reconstructed phase (segmented SSB)','reconstructed phase (segmented OBF)')
):
    py4DSTEM.show(
        np.tile(arr,(2,2)),
        figax=(fig,ax),
        cmap='turbo',
        ticks=False,
        title=title,
    )

for ax, arr in zip(
    axs[1],
    (np.angle(segmented_ssb.object),np.angle(segmented_obf.object))
):
    py4DSTEM.show(
        np.tile(arr,(2,2)),
        figax=(fig,ax),
        cmap='turbo',
        show_fft=True,
        apply_hanning_window=False,
        ticks=False,
    )

fig.tight_layout()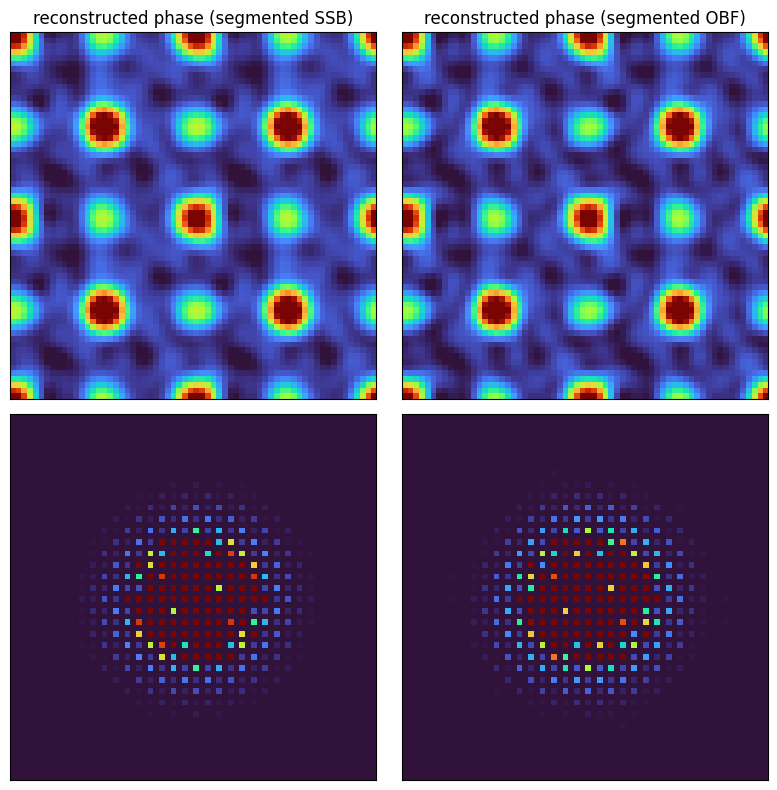
<Figure size 800x800 with 4 Axes>

Acknowledgments

This tutorial was created by the py4DSTEM phase_contrast team:

References
  1. Ooe, K., Seki, T., Ikuhara, Y., & Shibata, N. (2021). Ultra-high contrast STEM imaging for segmented/pixelated detectors by maximizing the signal-to-noise ratio. Ultramicroscopy, 220, 113133. 10.1016/j.ultramic.2020.113133
  2. Yang, H., MacLaren, I., Jones, L., Martinez, G. T., Simson, M., Huth, M., Ryll, H., Soltau, H., Sagawa, R., Kondo, Y., Ophus, C., Ercius, P., Jin, L., Kovács, A., & Nellist, P. D. (2017). Electron ptychographic phase imaging of light elements in crystalline materials using Wigner distribution deconvolution. Ultramicroscopy, 180, 173–179. 10.1016/j.ultramic.2017.02.006
Try it Yourself!
Direct Ptychography Tutorial 02
Try it Yourself!
Iterative Ptychography Tutorial 01
Colin Ophus Lab | StanfordColin Ophus Lab | Stanford
Understanding materials, atom by atom — Colin Ophus Lab
Lab Group Website by Curvenote
Stanford
University(link is external)
© Stanford University.  Stanford, California 94305.