Contents
Iterative Ptychography
While direct ptychography offers dose-efficient imaging at high resolution, iterative ptychography has distinct advantages over it Rodenburg & Faulkner, 2004:
- It can solve for both the object and the often unknown probe illumination
- It relaxes stringent sampling constraints by allowing redundancy with defocused probes
- It is very flexible and easy to adapt to incorporate additional physics (e.g. multi-slice, mixed-state, etc.)
Ptychographic Iterative Engine Demo¶
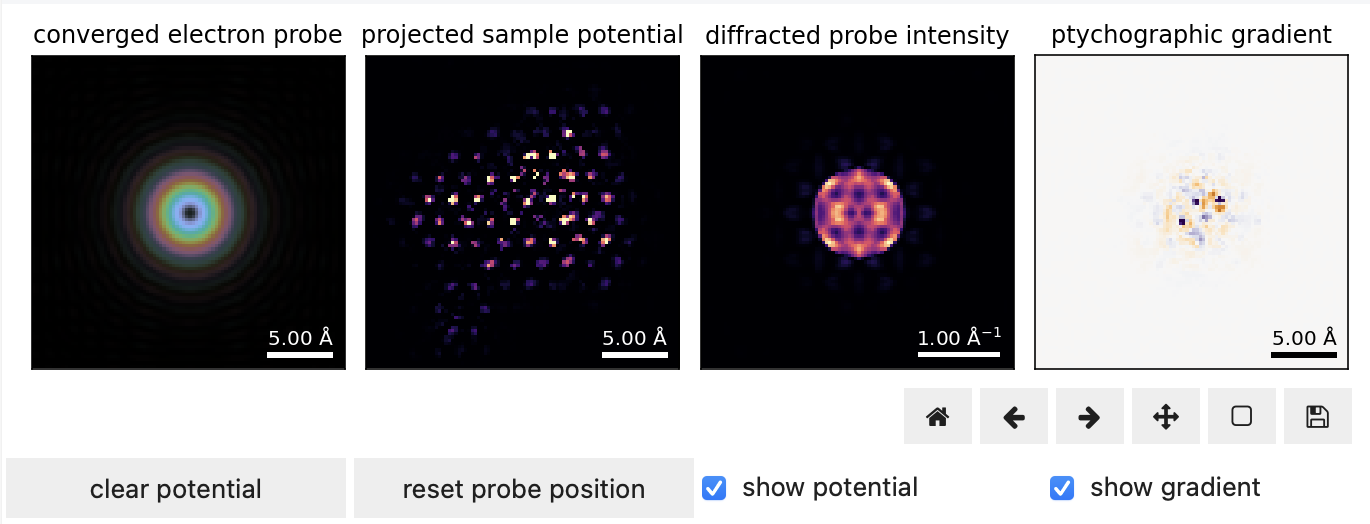
Figure 13.1 illustrates the main idea of model-based inversion algorithms like ptychography for a thin sample of Au viewed along the [111] zone axis, for a popular serial ptychography algorithm called ePIE Maiden & Rodenburg, 2009.
Source:Iterative Ptychography
VBox(children=(Canvas(footer_visible=False, header_visible=False, layout=Layout(height='225px', width='680px')…Figure 13.1:Iterative electron ptychography.
- We start by positioning a guess for the incoming probe on an empty “object” (here, the projected scattering potential)
- We then use our forward model to compute an estimate for the complex-valued exit wave
- We use this to compute the gradient between our estimate for the diffraction intensities and the measured data
- This is commonly performed in Fourier-space by replacing the amplitude of our modeled exit wave with the square-root of the measured intensities
- The real-space gradient, which has both positive and negative contributions, is added back to the guesses for the potential and the probe
- Optionally, we can constrain our potential and/or our probe guesses
- For example, since we expect the imparted phase-shifts to be positive, we can clip any negative values from our object
- The above steps are repeated for all probe positions at random, iterating as needed for convergence
Forward Model Extensions¶
Depending on the type of assumptions we make for the scattering physics, we are able to reconstruct increasingly complex samples and phenomena using appropriate forward and adjoint models. Table 13.1 summarizes these phenomena and provides some of the relevant citations:
Table 13.1:Iterative Ptychography Extensions
| Applicability/Physical Phenomenon | Conventional Name/Reference |
|---|---|
| Thin or weakly-scattering objects | Single-slice ptychography Maiden & Rodenburg, 2009 |
| ‘Thick’ or multiply-scattering objects | Multi-slice ptychography Chen et al., 2021 |
| Partial probe coherence | Mixed-state ptychography Thibault & Menzel, 2013 |
| Tilt-series of ‘thick’ objects | Joint ptychographic tomography Lee et al., 2023 |
| Incoherent (e.g. thermal) scattering | Open question in the field! |
- Rodenburg, J. M., & Faulkner, H. M. L. (2004). A phase retrieval algorithm for shifting illumination. Applied Physics Letters, 85(20), 4795–4797. 10.1063/1.1823034
- Maiden, A. M., & Rodenburg, J. M. (2009). An improved ptychographical phase retrieval algorithm for diffractive imaging. Ultramicroscopy, 109(10), 1256–1262. 10.1016/j.ultramic.2009.05.012
- Chen, Z., Jiang, Y., Shao, Y.-T., Holtz, M. E., Odstrčil, M., Guizar-Sicairos, M., Hanke, I., Ganschow, S., Schlom, D. G., & Muller, D. A. (2021). Electron ptychography achieves atomic-resolution limits set by lattice vibrations. Science, 372(6544), 826–831. 10.1126/science.abg2533
- Thibault, P., & Menzel, A. (2013). Reconstructing state mixtures from diffraction measurements. Nature, 494(7435), 68–71. 10.1038/nature11806
- Lee, J., Lee, M., Park, Y., Ophus, C., & Yang, Y. (2023). Multislice Electron Tomography Using Four-Dimensional Scanning Transmission Electron Microscopy. Physical Review Applied, 19(5). 10.1103/physrevapplied.19.054062
